Mécanismes et limites de la croissance exponentielle¶
Auteurs et date
- Date de production de la fiche : 31/05/2021
- Martine Olivi ; Chargée de recherche chez Inria
Toujours plus vite¶
C'est ainsi qu'on peut qualifier la croissance exponentielle. La croissance linéaire et la croissance exponentielle sont deux modèles mathématiques simples et pertinents, des repères essentiels dans la jungle des comportements évolutifs observés dans le monde réel. Dans une croissance linéaire, l'accroissement par unité de temps est un nombre fixe : par exemple le diamètre d'un arbre croit de 5 cm par an, indépendamment de sa taille. Dans une croissance exponentielle, l'accroissement par unité de temps est proportionnel à la quantité : par exemple l'évolution du nombre de personnes contaminées par un virus dépend du nombre de personnes contaminées. C'est l'effet boule de neige.

Voir la formulation mathématique
Si \(x_n\) désigne la quantité mesurée l'année \(n\), et \(a\) le coefficient de proportionnalité ou taux de croissance, la croissance exponentielle s'exprime par la relation
\(x_{n+1}-x_n= a\, x_{n}\)
La suite \((x_n)\) est une suite géométrique : \(x_{n+1}= (1+a)\, x_{n}\) de raison \(1+a\) supérieure à \(1\), le fameux \(R\) des modèles d'épidémiologie. Lorsque \(a\) est positif, plus la quantité est importante, plus elle augmente.
> « Plus vite, plus grand, plus beau : pendant plusieurs décennies, les lois de Moore ont gouverné la croissance exponentielle des performances de l’informatique, avec une sensation de progrès plus forte que dans aucun autre secteur. » Cédric Villani.
La part des émissions mondiales de GES due au numérique croit aujourd'hui de 6% par an, c'est-à-dire qu'elle est multipliée par 1,06 chaque année. Au bout de deux ans elle sera multipliée par \(1,06^2=1,1236\). Par exemple, la quantité de données échangées sur les réseaux mobiles double tous les 3 ans ! Là, on y voit un peu plus clair, on sait qu'une quantité qui double à intervalles de temps réguliers va vite devenir faramineuse, comme l'illustre le problème de l'échiquier de Sissa, ou celui de la croissance des nénuphars1. Calculer le temps de doublement d'une quantité permet de mieux se représenter une croissance exponentielle. Au rythme de 6% par an, la part des émissions mondiales de GES dues au numérique devrait donc doubler d'ici 12 ans (\(1,06^12 = 2,0122\)). Cela voudrait dire que dans les 12 prochaines années, le numérique émettrait autant de GES qu'il en a émis à ce jour depuis le début de la révolution numérique. Ses émissions représenteraient alors 7% des émissions mondiales de GES, alors qu'elles sont aujourd'hui à 3,5%. Et c'est compter sans l'augmentation probable de ce taux de croissance 2.
Mais au fond, pourquoi cette croissance vertigineuse se poursuit-elle alors que les progrès techniques rendent nos équipements de plus en plus performants d'un point de vue énergétique ? Cela s'explique de la façon suivante 2: l'amélioration des performances techniques induit une augmentation des usages, laquelle suscite de nouvelles améliorations, etc. Il s'agit d'une boucle de rétroaction positive qui stimule la croissance. L'augmentation de la consommation énergétique causée par l'augmentation des usages, compense largement les économies d'énergies dues aux améliorations techniques. C'est ce qu'on appelle un effet rebond (voir la fiche concept "L’effet rebond"fiche concept "L’effet rebond").
Cercle vicieux ou vertueux ?¶
Selon Olivier Hamant, directeur de recherche à INRAE,
> « La rétroaction est un concept clé pour comprendre le vivant, de la cellule à la planète »
Ce concept est en outre plus pertinent que celui de causalité pour décrire le comportement d’un système complexe. On distingue les rétroactions positives qui provoquent une accentuation du phénomène, voire un emballement. Une petite perturbation peut alors déclencher une croissance exponentielle des quantités en jeu. Les rétroactions négatives au contraire s'opposent au phénomène qui les a engendrées et peuvent le réguler, ou le réduire à néant.
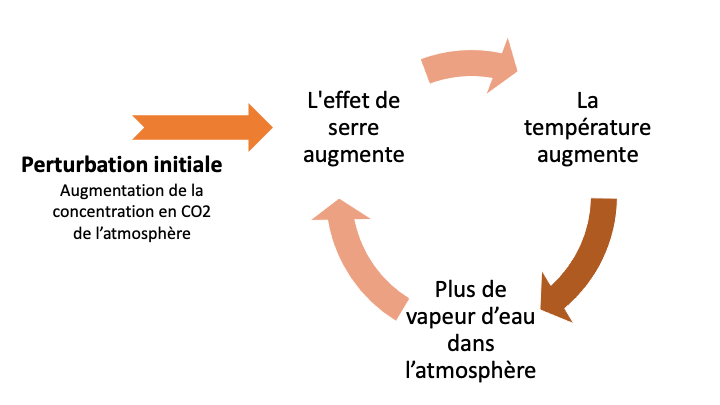
Dans les modèles du climat, on trouve de nombreuses boucles de rétroaction. Un exemple classique est celui de la vapeur d'eau. L'augmentation du CO2 dans l'atmosphère (perturbation initiale) conduit à une augmentation de la température globale. Lorsque la température augmente, la concentration en vapeur d'eau de l'atmosphère augmente à son tour. Il y a plus d'humidité dans l'air. Mais la vapeur d'eau est un puissant gaz à effet de serre. Si la quantité de vapeur d'eau dans l'atmosphère augmente, cela va provoquer une élévation de la température et ainsi de suite.
Les cas des nuages est particulièrement intéressant, car il constitue un défi pour les climatologues. Les nuages de la basse atmosphère réfléchissent une partie du rayonnement solaire et contribuent au refroidissement de la planète, tandis que les nuages de la haute atmosphère contribuent à l'effet de serre. Mais les variations de la couche nuageuse dues au réchauffement climatique sont encore mal comprises, et les scientifiques ne savent pas à ce jour si au final les nuages contribuent à une rétroaction positive ou négative3.
Une vidéo de SimClimat4 montre l'importance de la prise en compte de ces phénomènes de rétroaction dans les modèles du climat et explique comment vérifier que ces modèles ont été correctement calibrés, c'est à dire que les paramètres extérieurs au modèle ont été correctement choisis.
Aplatir l'exponentielle.¶
> « Je peux vous dire en tant que biologiste que toutes les courbes exponentielles que nous observons dans le monde végétal et dans le monde animal parmi les êtres vivants, finissent toujours extrêmement mal. Le cas où ça se passe moins mal, c'est lorsqu'il y a une stabilisation. »
C'est ce que disait Jean Dorst, ornithologue français, dans l'émission Demain la terre du 13/04/19745. Mais comment stabiliser la croissance ? Comment aplatir l'exponentielle ?
Le mathématicien belge Pierre-François Verhulst (1804-1849), chercha une réponse mathématique à ce problème, soulevé par Malthus à la fin du 18ème, lequel s'émouvait de la croissance exponentielle de la population humaine. Verhulst proposa une autre forme de croissance, la croissance logistique. Ce que nous dit ce modèle, c'est qu'une croissance exponentielle confrontée à des limites (nourriture, espace) se régule automatiquement.
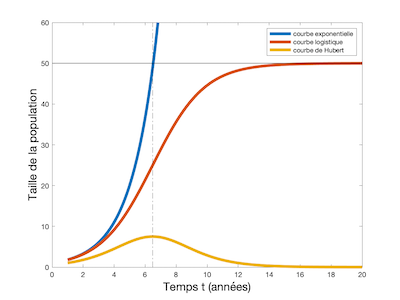
Le modèle de Verhulst est en temps continu : le temps y est représenté par une variable réelle, \(t\), et la population à l'instant \(t\) est donnée par une fonction mathématique, c'est-à-dire un processus qui à la variable \(t\) fait correspondre une quantité notée \(f(t)\). La courbe représentative de la fonction \(f\) a une forme caractéristique en \(S\), encore appelée sigmoïde. Elle commence à croître comme une exponentielle lorsque la population est encore petite, puis la courbure s'inverse et la courbe se rapproche d'une valeur limite \(K\) sans jamais l'atteindre.
Voir la formulation mathématique
La fonction \(f\) est la solution d'une équation qui relie l'accroissement instantané de la population à la population elle-même. L'accroissement instantané doit être pensé comme la vitesse de croissance de la population et il correspond à une opération mathématique, la dérivée ou différentielle, notée \(f'\). L'équation logistique est :
\(f'(t)= a\, f(t)\, (1- f(t)/K).\)
La croissance exponentielle y est régulée par une rétroaction négative (le signe - dans l'équation), qui fait intervenir un paramètre \(K\), appelé capacité de charge. Lorsque cette capacité tend vers l'infini, le terme négatif tend vers \(0\) et on retrouve la croissance exponentielle :
\(f'(t)= a \,f(t).\)
En pratique, les deux paramètres \(a\) et \(K\) doivent être ajustés à partir de données réelles de la même façon que l'on ajuste la pente d'une droite passant par des points qui semblent alignés (régression linéaire). L'accroissement instantané, la fonction dérivée \(f'\), a une courbe représentative en forme de cloche, symétrique par rapport à son maximum, connue sous le nom de courbe de Hubert.
Le géophysicien américain Marion King Hubert trouva la fonction logistique pertinente pour représenter l'extraction cumulée de pétrole, laquelle est clairement limitée par la quantité totale de pétrole existant. Hubert en déduisit que la production de pétrole, représentée par la courbe en forme de cloche qui porte aujourd'hui son nom, passe par un pic avant de chuter. Il avait même estimé que la production de pétrole aux Etats-Unis passerait par un pic en 1970 !
Le modèle logistique, modèle phare de la dynamique des populations, a aussi été utilisé pour analyser l'épuisement des ressources ou illustrer la diffusion d'une innovation. Mais bien sûr un modèle aussi simple ne donne qu'une représentation grossière de la réalité, et ne permet pas de prédictions précises. Il permet toutefois d'estimer des échelles de temps et soulève des questions fondamentales 6.
Des modèles à l'échelle planétaire¶
> «Essentially all models are wrong but some are useful.» George E. P. Box
Une de ces questions fondamentales est la suivante : les ressources planétaires étant limitées, est ce que la population humaine va gentiment suivre une courbe logistique et se stabiliser autour de sa capacité de charge maximale ou la dépasser puis chuter plus ou moins brutalement ?
Pour répondre à cette question, des chercheurs du MIT ont conçu le modèle mathématique World3, qui a servi à l'écriture du livre "The Limits to Growth" (1972). Ce modèle relève d'une discipline toute jeune, la dynamique des systèmes, née dans les années 50 au MIT. L'avènement des premiers ordinateurs autorise alors les chercheurs à s'attaquer à des problèmes complexes, ici à l'échelle planétaire et sur des temps longs. D'après ce modèle, la croissance exponentielle de la production industrielle pourrait effectivement conduire à un dépassement des capacités de charge, et un effondrement, qu'il faut entendre comme une chute, plus ou moins rapide, de la population et de la production.
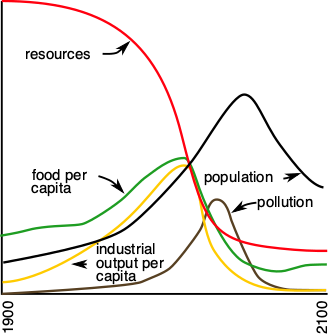
Dans World3, le "système monde" est représenté par des réservoirs (population, capital, ressources naturelles et non-naturelles, richesses, pollution), qui communiquent entre eux par des flux de matières et des effets positifs ou négatifs. Ce modèle est fondé sur l'hypothèse d'une capacité maximale de la planète à produire certaines ressources indispensables à l'humanité. Les interactions sont régies par des lois mathématiques simples, comme la croissance logistique.
Il s'agit donc d'un modèle extrêmement simplifié, qui agrège des réalités bien différentes sous une même bannière. Il n'y a pas non plus de moyen rigoureux de vérifier la calibration du modèle : le choix des paramètres clefs et des différentes rétroactions. Cependant, il colle assez bien aux mesures réelles observées depuis, et il fournit des indices intéressants comme l'inertie du système monde ou le rôle majeur de la pollution dans un certain nombre de rétroactions négatives. Comme le souligne cette vidéo de Heu?reka7, il porte un message qui parle aux scientifiques : l'humanité doit se donner des objectifs de développement en accord avec les contraintes de la nature. Il a aussi promu une approche systémique des questions environnementales.
À partir des années 50 l'approche systémique, jusque là plutôt réservée à l'ingénierie, s'est répandue à d'autres domaines ; l'évolution du développement humain comme nous venons de le voir, mais aussi l'étude du climat qu'il ne faut pas confondre avec la météo. Dans l'étude du climat, on s'intéresse à des moyennes, des statistiques, pas à des évènements localisés ou ponctuels. Historiquement, le premier modèle atmosphérique date de 1950, et a été testé sur le premier ordinateur existant, l'ENIAC. Depuis lors, les modèles de climat n'ont cessé de s'enrichir et incluent maintenant cinq composantes principales : l'atmosphère, les surfaces continentales, l'hydrosphère, la cryosphère, et la biosphère. Ces composantes échangeant entre elles en eau, chaleur, composés chimiques, ...
Contrairement au modèle World3, les équations qui régissent les interactions entre les différentes grandeurs caractéristiques, sont les équations de la physique, et les paramètres clefs sont calibrés sur des données historiques. La résolution numérique de ces équations complexes nécessite le découpage de la surface de la terre, des océans et de l'atmosphère en petits cubes qu'on appelle les mailles. Plus les mailles sont petites, plus les calculs sont précis et fiables. Le nombre de mailles utilisé dans les modèles de climat a augmenté de façon exponentielle au fil des années ! Aujourd'hui une quarantaine de modèles différents sont développés dans le monde, dont celui de l'Institut Pierre-Simon Laplace (IPSL) en France. L'IPSL propose une version simplifiée de son modèle à usage pédagogique8.
Les émissions de GES apparaissent comme des perturbations extérieures au système, et ces modèles simulent les différents scénarios de réduction de ces émissions, qui ont été présentés dans les différents rapports du GIEC. Ces modèles sont imparfaits, parce que certains phénomènes physiques sont encore mal compris et à cause des incertitudes liées aux modélisations numériques. Mais là encore, l'objectif n'est pas de faire des prévisions quantitatives, mais d'obtenir des ordres de grandeurs, qui permettent de comprendre l'influence sur le climat de nos choix de développement. Et ils jouent parfaitement ce rôle.
Lexique¶
Accroissement instantané : variation d'une quantité qui varie au cours du temps rapporté à une variation de infinitésimale de temps
Biosphère : tous les organismes vivants dans l'air, sur terre et dans les océans
CMIP : Coupled Model Intercomparison Project. Ce projet vise à réaliser des simulations climatiques de façons coordonnée entre les différents groupes de recherche permettant une meilleure estimation et compréhension des différences entre les modèles climatiques wikipedia
Cryosphère : les glaces terrestres ou marines, le manteau neigeux
Hydrosphère : les océans, lacs, rivières, nappes d'eau souterraines ...
Rétroaction : action en retour d’un effet sur le mécanisme qui lui a donné naissance.
Système : un ensemble d'éléments interagissant entre eux selon certains principes ou règles. Un système composé d'un grand nombre d'éléments et d'interaction est qualifié de complexe.
Bibiographie¶
Articles¶
- Cedric Villani. L’informatique durable n’existe pas encore [en ligne]. Libération, 2021. Disponible sur le site de Libération [20/07/2021]
- Martine Olivi. Des expériences pour mieux appréhender la croissance exponentielle [en ligne]. Pixees, 2020. Disponible sur Pixees [20/07/2021]
- Olivier Hamant. La rétroaction, un concept clé pour comprendre le vivant, de la cellule à la planète [en ligne]. Inrae, 2020. Disponible sur le site d'Inrae [20/07/2021]
- Laurent Li. Les rétroactions sont-elles prises en compte dans les modèles ? [en ligne]. Le climat en questions (IPSL), 2014. Disponible sur le site Le climat en questions [20/07/2021]
- Sylvain Barré. Inverser la courbe [en ligne]. Image des Maths (CNRS), 2014. Disponible sur le site Images des Mathématiques [20/07/2021]
- José Halloy. L’épuisement des ressources minérales et la notion de matériaux critiques [en ligne]. La rue nouvelle, 2018. Disponible sur le site revuenouvelle.be [20/07/2021]
- Daniel Perrin. La suite logistique et le chaos [en ligne]. Département de Mathématiques d'Orsay, 2008. téléchargeable sur [20/07/2021]
Infographie¶
- Shift Project. Impact environnement du numérique, tendance à 5 ans et gouvernance de la 5G, 2021, url
Ouvrages¶
- Donella Meadows, Jorgens Randers, Dennis Meadows. Limits to Growth - The 30-Years Update [en ligne]. Dennis Meadows, 2004. Disponible sur [20/07/2021]
Pages web¶
- Insightmaker, The World3 Model Classic World Simulation, url
- Laboratoire de Météorologie Dynamique, SimClimat: un logiciel pédagogique de simulation du climat, mise à jour 2020, url
Podcasts¶
- Hélène Combris. Le jour du dépassement recule de trois semaines. France Culture, Covid-19, retour sur Demain la terre du 13/04/1974, mis à jour 2020 url [20/07/2021]
Rapports¶
- GreenIT, Empreinte mondiale du numérique, 2019 url
- Shift project, Déployer la sobriété numérique, 2020, url
Vidéos¶
- Rodolphe Meyer, Le réveilleur. Modèles climatiques, 2016, 10:30. url
- Institut Pierre-Simon Laplace (IPSL), Tutoriel SimClimat no 3 : Les rétroactions climatiques, 2020. 9:16. url
- Gilles Mitteau, Heu?reka: Modéliser l'avenir de l'humanité, 2020. 1:13:15. url
Sources¶
-
Martine Olivi, Des expériences pour mieux appréhender la croissance exponentielle, Pixees, 2020, url ↩
-
Shift project, Impact environnemental du numérique :tendances à 5 ans et gouvernance de la 5G, 2021, url ↩↩
-
Laurent Li, Les rétroactions sont-elles prises en compte dans les modèles ?, Le climat en questions (IPSL), 2014, url ↩
-
Institut Pierre-Simon Laplace (IPSL), Tutoriel SimClimat no 3: Les rétroactions climatiques, 2020, url ↩
-
France Culture, Covid-19 : le jour du dépassement recule de trois semaines par Hélène Combris (retour sur Demain la terre du 13/04/1974), mis à jour 2020 url ↩
-
José Halloy, L’épuisement des ressources minérales et la notion de matériaux critiques, La rue nouvelle, 2018, url ↩
-
Gilles Mitteau, Heu?reka: Modéliser l'avenir de l'humanité, 2020 url ↩
-
Laboratoire de Météorologie Dynamique, SimClimat: un logiciel pédagogique de simulation du climat, mise à jour 2020, url ↩
