La simulation numérique, un outil devenu central pour l'environnement¶
Auteurs et date
- Date de production de la fiche : 5/9/2021
- Eric Blayo ; professeur en mathématiques appliquées, Université Grenoble Alpes
Introduction¶
Quand on évoque la simulation numérique pour l'environnement, on pense souvent en tout premier lieu aux projections climatiques dont le GIEC présente régulièrement la synthèse, comme cela a déjà été évoqué dans ce MOOC. Mais ce sont en fait de multiples questions environnementales pour lesquelles les modèles numériques fournissent une aide cruciale à la compréhension et à la décision.
Cette fiche concept va tenter de préciser ce qu'est la simulation numérique au-delà de l'idée plus ou moins vague que l'on peut tous en avoir, et comment elle s'est développée dans le domaine environnemental pour de nombreuses applications.
Modéliser : une vision mathématique du monde réel¶
Modéliser un système, qu'il s'agisse de la structure d'un pont, du flux de clients aux caisses d'un supermarché, ou du climat terrestre, c'est avant tout formaliser les grands principes qui en régissent le comportement, et les traduire par des équations mathématiques. Dans les domaines liés aux sciences dites « dures », ces principes sont plutôt bien connus : conservation de la masse et/ou de l'énergie, transformations chimiques, relations entre espèces... En mécanique des fluides, en première ligne pour de nombreuses questions environnementales (atmosphère, océan, rivières...), les travaux de grands scientifiques comme Euler, Fourier, Navier, Stokes, Coriolis ou Boussinesq ont posé les bases de telles équations depuis deux siècles. Pour d'autres types de systèmes complexes comme la végétation ou l'économie, cette description mathématique est moins avancée, même si la connaissance progresse constamment.
Cependant, la complexité de ces modèles mathématiques est souvent telle qu'il est impossible de résoudre de façon exacte leurs équations1. On peut par contre en chercher des solutions approchées (mais pas approximatives !) grâce aux techniques de simulation numérique. L'idée de base consiste à découper l'objet auquel on s'intéresse (pont, pièce mécanique, atmosphère terrestre) en « briques élémentaires » (le maillage de l'objet) et à rechercher une valeur des quantités physiques d'intérêt dans chaque maille, en remplaçant les équations par une version simplifiée (les équations discrétisées) ne faisant plus intervenir que les valeurs dans les mailles voisines, reliées par des opérations arithmétiques2. On substitue ainsi à chaque équation initiale complexe un système d'équations (une par maille) très simples, dont les inconnues sont les valeurs des variables physiques (température, concentrations chimiques...) dans chaque maille. Il ne reste alors qu'à résoudre cet ensemble d'équations simples, ce qui peut tout de même nécessiter un ordinateur puissant si l'on doit faire usage d'un grand nombre de mailles3.
Cette méthodologie est toujours à peu près la même, que l'on s'intéresse à simuler le climat terrestre ou un écoulement de pâte à biscuits dans une usine alimentaire.

Figure 1 Maillage tridimensionnel de la composante atmosphérique d'un modèle de climat. Les couleurs représentent la température et les flèches le vent. © Vincent Landrin, d'après Laurent Fairhead/LMD/CNRS
Le modèle numérique : jeu vidéo ou outil scientifique ?¶
On dispose à ce stade d'un outil numérique visant à fournir un avatar d'un système réel. Rien ne garantit toutefois sa qualité : cliquer sur le bouton « start » lui fera toujours créer des résultats, qui pourront être mis en valeur par de superbes animations 3D. Mais la qualité d'un rendu visuel ne fait pas la qualité scientifique (même si le rendu peut bien sûr être important pour aider le scientifique à comprendre et exploiter les résultats de la simulation, ainsi qu'à des fins de médiation vers le grand public). Plusieurs étapes sont donc encore nécessaires pour que le modèle numérique devienne un réel outil scientifique.
Un premier enjeu fort est de garantir que la solution numérique obtenue soit une bonne approximation de la solution des équations complexes de départ. Cette assurance est obtenue par différentes techniques mathématiques utilisées tout au long du processus de modélisation et de calcul.
Pour que le modèle numérique soit réaliste, il faut aussi « régler ses boutons », c'est-à-dire les paramètres physiques et numériques intervenant dans le modèle dont les valeurs ne sont pas forcément bien connues. Ce réglage est réalisé en comparant les résultats du modèle à des observations de la réalité et/ou à différents critères physiques. Des techniques mathématiques très sophistiquées (méthodes inverses ou assimilation de données) peuvent être mises en œuvre pour déterminer de tels réglages optimaux. C'est ce que font par exemple quotidiennement tous les centres de prévision météorologique en « assimilant » des millions de mesures atmosphériques réalisées lors des dernières 24 ou 48 heures, afin de déterminer de façon précise l'état courant de l'atmosphère, qui sera le point de départ pour la prévision sur les jours suivants.
Enfin, une information particulièrement utile à l'utilisateur d'un modèle numérique est le niveau de confiance qu'il peut avoir dans ses résultats. Un bon modèle cherche donc à fournir également une estimation de l'incertitude sur ses résultats, qui peut aller d'un simple indicateur qualitatif (un indice de confiance) à une description probabiliste de l'étendue des possibles.
Simulation numérique pour le climat¶
Du fait de son intérêt pratique évident, la prévision météorologique a été un domaine précurseur de la simulation numérique. Depuis la première prévision numérique du temps par Charney et Von Neumann4 à la fin des années 40, qui s'inspirait des travaux visionnaires de Richardson5, les modèles furent sans cesse améliorés, et ce savoir-faire se diffusa parmi les géophysiciens et accéléra grandement le développement de modèles numériques dans des disciplines connexes : premiers modèles de la circulation océanique et du climat dans les années 70, puis hydrologie, glaciologie, etc.
Décrire le climat, c'est expliciter le fonctionnement de ses principales composantes : atmosphère et océan, mais aussi cryosphère, rivières, sols, biosphère... Autant de « compartiments » dont il faut de plus expliciter les interactions (échanges d'énergie, d'eau, de carbone...). Insistons sur un point fondamental : même s'il est intrinsèquement impossible de prévoir la météo au-delà d'une échéance de l'ordre de 15 jours6, son comportement statistique (c'est-à-dire le climat) est par contre tout à fait prévisible plusieurs dizaines d'années à l'avance. Ceci est du même ordre que prévoir précisément l'évolution de la température moyenne dans une casserole d'eau sur une cuisinière à gaz selon le réglage de la flamme, alors qu'on est incapable d'anticiper le comportement exact de chaque molécule.
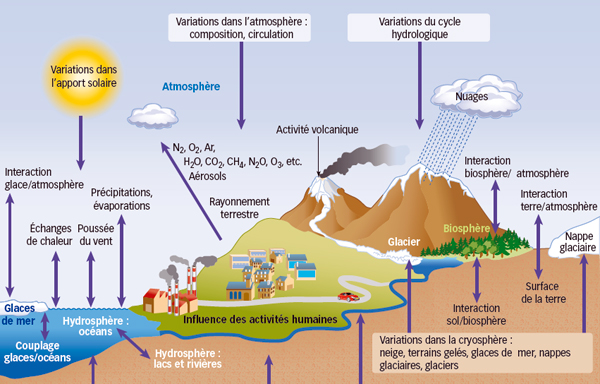
Figure 2 Les principales composantes du système climatique et leurs interactions. © Vincent Landrin (source : 4e rapport du GIEC).
La mise en œuvre informatique des modèles de climat est un véritable défi. Le comportement du système climatique, même à grande échelle, est en effet largement influencé par les phénomènes de plus petite échelle. Il est donc théoriquement nécessaire d'utiliser une résolution spatiale suffisamment fine, idéalement de l'ordre de quelques kilomètres pour l'atmosphère, et encore plus fine pour l'océan. Mais le nombre d'équations discrétisées à résoudre dépasseraient alors très largement les capacités des plus puissants supercalculateurs. La résolution des modèles climatiques est donc fixée pour l'instant, et le sera encore longtemps, en fonction de la puissance de calcul disponible. Elle est actuellement relativement faible : de l'ordre de 50 à 100 km sur l'horizontale pour l'atmosphère et l'océan, et quelques dizaines à centaines de mètres sur la verticale. Les plus fines échelles spatiales ne sont pas présentes dans ces modèles, et leur effet sur le climat à plus grande échelle ne peut qu'être simulé de façon imparfaite, au moyen de termes ad hoc ajoutés aux équations. Mais même avec cette résolution insuffisante, les modèles calculent l'évolution de plusieurs dizaines à centaines de millions de variables, sur des durées de dizaines d'années, à intervalle de quelques minutes ou dizaines de minutes, ce qui représente un volume de calcul gigantesque.
Les modèles numériques de climat sont réglés et validés en comparant leurs résultats aux observations disponibles, notamment celles, nombreuses, des décennies récentes. Une fois mis au point, ils peuvent alors fournir des projections sur les évolutions possibles du climat dans les décennies, voire les siècles, à venir. Ces études sont coordonnées au niveau international par le GIEC, créé en 1988 par l'ONU. Ce Groupe d'experts Intergouvernemental sur l'Evolution du Climat fournit des rapports de synthèse sur les connaissances scientifiques concernant le changement climatique. Plusieurs « futurs possibles » des sociétés humaines (développement économique et démographique, choix énergétiques, évolution des comportements individuels) sont traduits en termes de scénarios d'émissions de gaz à effet de serre. Les centres de recherche de par le monde simulent alors avec leurs différents modèles les évolutions climatiques qui en résulteraient. Une synthèse globale est ensuite réalisée afin de dégager des tendances fiables, et de quantifier les incertitudes autour de ces tendances.
Simulation numérique et environnement¶
Les applications des modèles numériques dans les domaines liés à l'environnement sont aujourd'hui innombrables, qu'il s'agisse de prévision à courte échéance (météorologie, qualité de l'air, risque inondation...), à moyen ou long terme (prévision saisonnière de la mousson ou d'El Niño, projections climatiques...), ou d'étude d'impact (comment évoluera l'ensablement si l'on construit une digue ? Quelles zones à risque en cas de rupture d'un barrage ?).
Au-delà de l'eau et de l'air, les modèles numériques sont également omniprésents dans le domaine du vivant : modèles écologiques étudiant l'évolution des populations de différentes espèces, biogéochimie marine, végétation, agriculture (optimisation des intrants, prévision des récoltes...). Ils sont aussi d'importants outils d'aide à la compréhension et à la décision pour les politiques publiques concernant par exemple l'organisation des sols et des transports.
Même s'il demeure des verrous scientifiques de modélisation et simulation, le numérique occupe donc une place centrale pour analyser de nombreuses questions environnementales (au premier rang desquelles l'évolution du climat), et participer à sensibiliser le public et à élaborer des actions politiques.
-
Il s'agit souvent d'équations aux dérivées partielles, pour lesquelles les solutions exactes ne sont connues que dans des cas particulièrement simples. ↩
-
Une méthode consiste par exemple à remplacer les dérivées par des taux d'accroissement. Ainsi la dérivée selon la direction x de la température au centre d'une maille numéro i pourra être approchée par le taux d'accroissement des températures des mailles de gauche (i-1) et de droite (i+1) : (dT/dx)i ~ (Ti+1-Ti-1)/(xi+1-xi-1) ↩
-
Un modèle météorologique opérationnel en compte couramment plusieurs dizaines ou centaines de millions. ↩
-
Charney J., R. Fjörtoft and J. Von Neumann, 1950: Numerical Integration of the Barotropic Vorticity Equation. Tellus A. 2. 10.3402/tellusa.v2i4.8607. ↩
-
Lewis Fry Richardson, 1922 : Weather Prediction by Numerical Process, Cambridge University Press. ↩
-
C'est le fameux effet papillon rendu célèbre par Edward Lorenz (1917 - 2008), qui illustre le caractère chaotique de la dynamique de l'atmosphère. Il en est de même d'ailleurs pour l'océan sur des échéances un peu plus longues. ↩